Research

This page provides a curated overview of my ongoing and past research projects. My work centers on leveraging techniques from information theory, coding theory, statistics, and probability to study foundational questions in privacy, cryptography, machine learning, and communication theory.

Graduate Research Summary

Efficient Representation of Information via Couplings

Consider a simple mathematical problem where, given multiple sources of randomness, the goal is to couple them in such a way that maximizes the statistical correlation between them. In mathematical terms, given 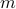random variables 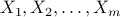X_1, X_2,dots, X_m , the goal is to find the joint distribution or coupling between them which minimizes the joint entropy 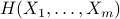H(X_1,dots, X_m) (equivalently maximizes the mutual information- a measure of correlation between random sources). This problem is commonly known as the Minimum Entropy Coupling (MEC) problem in probability theory.

A natural question that would arise here is, why would one care about finding such a coupling? It turns out that MEC sits at the heart of several problems in information and decision sciences. For instance, it is used to identify the direction of causality in entropic causal inference - the toolkit that allows for inferring the ‘causation’ between two random events, beyond mere association. In machine learning, it is used to pair the unlabeled multi-modal data obtained from multiple sources in order to ‘maximize’ the cross-modal correlation via mutual information, during the pre-training process, for better performance. In cryptography, using MEC during the encryption process allows to achieve a perfectly secure steganography. Other examples, where this problem is of interest, include optimal transport, dimensionality reduction, random number generation, etc.

As simple as the problem looks, solving it is deceptively difficult. The problem of finding the MEC is NP-Hard, i.e., no polynomial-time algorithm exists that can output the optimal coupling, say 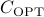$C_{mathrm{OPT}}$ . Our alternative approach is to first derive the worst-case guarantees on the MEC. Then, we analyze a polynomial-time approximation algorithm which outputs a coupling, say 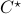$C^{star}$ , with entropy ‘close’ to the optimal solution. More specifically, given any random variables 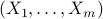(X_1,dots,X_m) , we show that

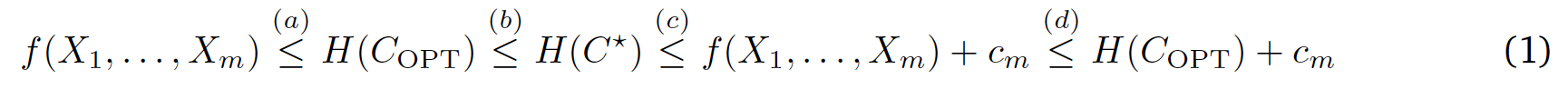
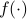First, we derive an easily computable function f(cdot)

that gives an information-theoretic lower bound on the entropy of the optimal coupling, i.e., Eq. 1(a)

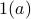. Then, we analyze a greedy-coupling algorithm and show that it outputs a coupling whose entropy is within c_m

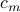(where

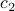approx.

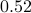and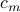

approx.

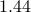for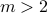

) bits of the lower bound, i.e., Eq. 1(c)

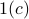. Together with Eq. 1(b)

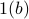and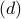

, we show that the entropy of 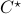$C^{star}$ is close to the optimal solution. Moreover, we prove our results for a broader class of entropies, namely the Rényi entropy 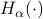$H_{alpha}(cdot)$ of any order alpha in [0,infty]

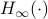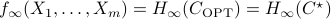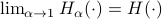. Our analysis shows that the greedy-coupling algorithm is optimal for infinite-order Rényi entropy $H_{infty}(cdot)$ , i.e., $f_{infty}(X_1,dots, X_m)=H_{infty}(C_{mathrm{OPT}})= H_{infty}(C^{star})$ . Note that $lim_{alpha rightarrow 1}H_{alpha}(cdot) = H(cdot)$ .

A related setting where the MECs show up is the Efficient Functional Representation of Information (EFRI). Given two correlated random variables 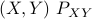$(X, Y)~ P_{XY}$ , the EFRI refers to finding a random variable 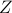with the least entropy 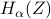$H_{alpha}(Z)$ , such that 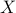is a deterministic function of 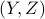(Y, Z) while 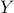and 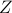are independent of each other. It is widely used to prove various results in {network information theory} and {wireless communications}. As it turns out from our analysis, solving the EFRI problem is equivalent to finding the MEC for the random variables 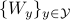${W_y}_{y in mathcal{Y}}$ such that 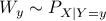$W_y sim P_{X|Y=y}$ . A line of work that we are currently exploring is lossless data compression under utility constraints, through EFRI, building on our result in Eq. .

Privacy-preserving Inference of Shifts in Information

Consider a scenario where the hospitals provide the city health office with daily patient-admission records. The objective is to detect an outbreak of a disease by tracking the admissions at the hospital for designated symptoms or diagnoses, and identifying statistically significant shifts in incidence. To achieve timely and reliable detection, the health office must deploy scalable algorithms that can detect changes in the available information with high accuracy and low detection delay, without raising false alarms. This process of inferring changes in the underlying information is commonly known as Change-Point Detection (CPD).

CPD is a widely studied concept in statistical theory with the goal of detecting and estimating the change point in a time series of data under the accuracy-latency tradeoff. Depending on how the data is available, i.e., in batches (offline data) or a sequential time-series (online data), or if the data is hypothesized to be sampled from a population or otherwise (parametric vs non-parametric setting), several task-aware CPD algorithms have been studied in the literature. They are widely used for monitoring the stock market, IoT-based surveillance, traffic and mobility, e-commerce, supply chains, etc. During my internship at the Nokia Bell Labs, we designed non-parametric CPD algorithms for in-vivo health monitoring in a Passive Optical Network. These methods support early detection of communication-link quality degradations and facilitate their root-cause identification.

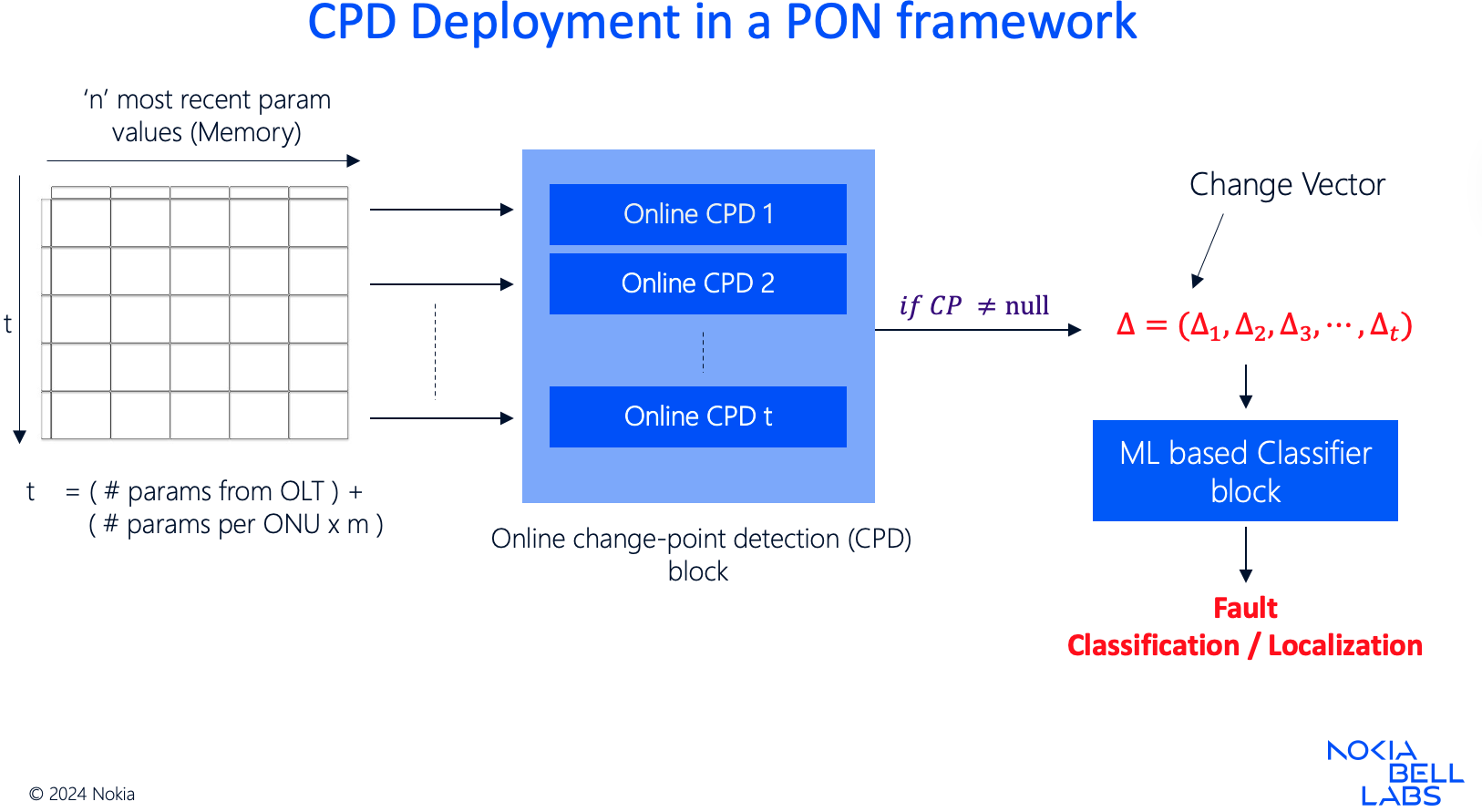
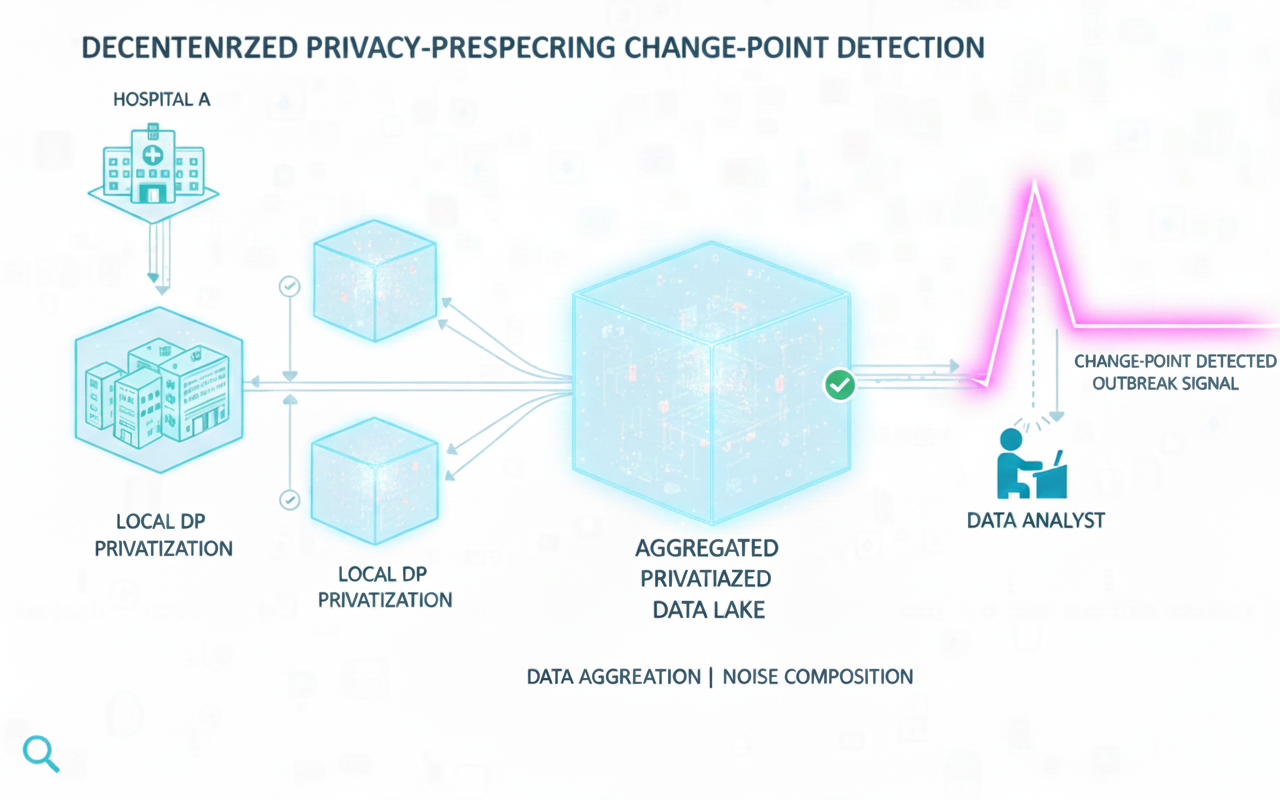
With the growing concerns regarding the misuse of personal data in today’s era, it is often undesirable to disclose sensitive information directly to the data analyst. This motivates the study of CPD in a privacy-preserving manner. We employ the notion of Differential Privacy, which is widely adopted in industry. We focus on studying fundamental limits and designing CPD algorithms under differential privacy, where the sensitive data is privatized at the source before being shared with the data analyst for the estimation of the change-point. Apart from the latency constraint, this framework introduces an added privacy constraint. Thus, our current work involves designing differentially private CPD algorithms, studying their accuracy-latency-privacy tradeoffs, and quantifying the cost of privacy.

Undergraduate Research Summary

Information-theoretic Cryptography

With rapid progress in computing technologies—most notably the emergence of quantum computing—the security foundations of many widely deployed cryptographic schemes are becoming increasingly vulnerable. Classical systems like RSA rely on computational hardness assumptions, but quantum algorithms threaten to undermine these assumptions entirely. As a result, such cryptosystems may become impractical or insecure in the near future. This motivates a stronger shift toward information-theoretically secure cryptography, where security holds unconditionally, regardless of an adversary’s computational resources. While these schemes are traditionally considered difficult to implement and less practical than computationally secure alternatives, they may soon be essential. Since cryptographic protocols are ultimately realized in physical systems, one promising approach is to exploit inherent noise or other imperfect resources to achieve unconditional security.

Our current research focuses on two fundamental primitives—bit commitment and oblivious transfer (OT). We investigate their fundamental performance limits and characterize both possibility and impossibility results under various noisy-channel models. We also design computationally efficient, capacity-achieving protocols that provide information-theoretic security by leveraging different classes of noisy channels extensively studied within information theory.

Bit Commitment

Bit Commitment is a widely studied cryptographic primitive with multitudinous applications in secure Multiparty Computation (MPC), blockchains, zero-knowledge proofs, sealed-bid auctions, etc. Consider two siblings, Alice and Bob, who are playing a game of chess. However, it’s late at night, so they decide to adjourn the game and continue in the morning. But, there’s a problem! Who makes the last turn? If it is Alice, Bob has the entire night to think about his turn until the next morning, leading to an unfair advantage; similarly is the case is if Bob makes the last turn.

A possible solution to this problem is that both of them can reach out to their mom and say that Alice covertly reveals her move to their mom, that she is going to make the next morning. The next day, when they continue the game, Alice is bound to make the same move, as Bob can verify it by asking Mom. Therefore, it ensures fair play in the game in the presence of mom - “a third party”. However, in a real-world scenario, the third party might not be available or its availability might be costlier. Therefore, can we achieve this kind of functionality without a third party?

The answer to this question lies in the Commitment Protocol, which was introduced by [Blum] as a computationally secure model that is based on computational assumptions on the users participating in the protocol. Crepeau et.al designed unconditionally secure or information-theoretically secure commitment protocols with the use of noisy channels. Such unconditionally secure commitment protocols are simply unbreakable even if the adversaries have infinite computing power and time.

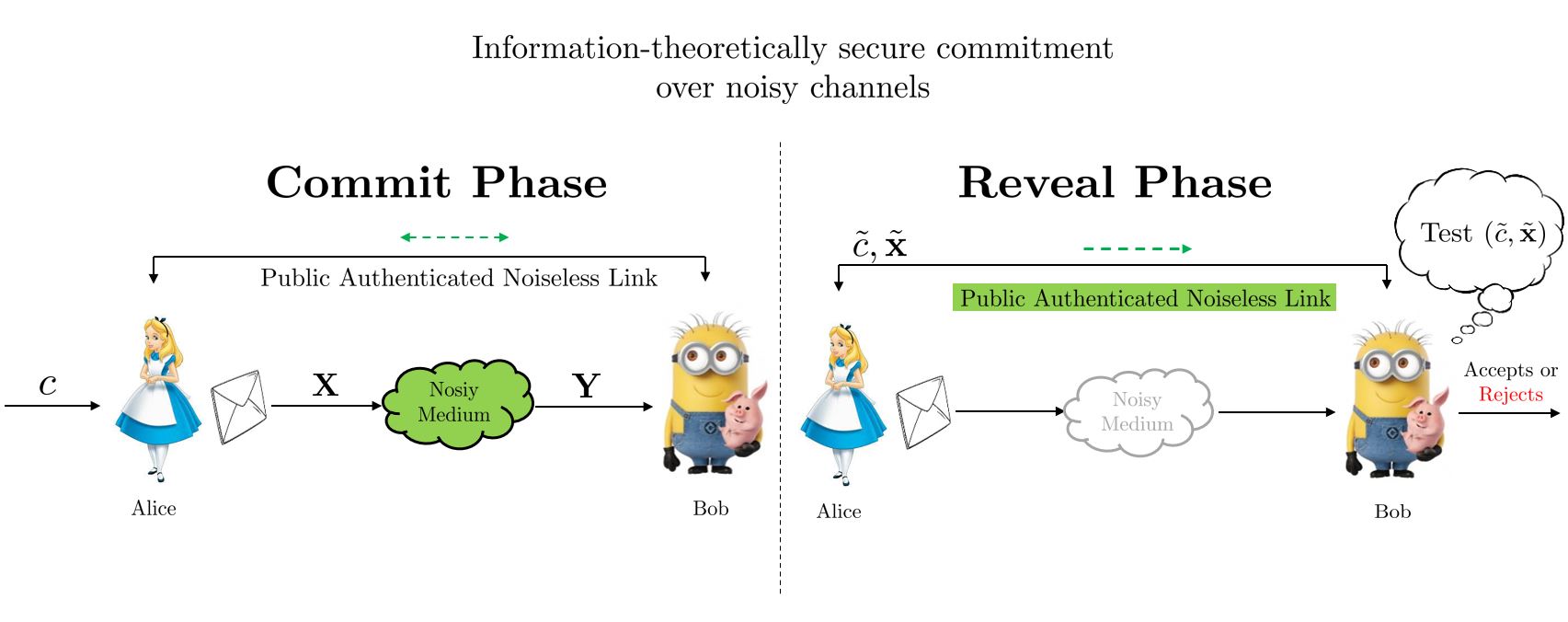
Specifically, we have studied Commitment over Discrete Memoryless Channels (DMCs) under input cost constraints and characterized its primal and dual capacity expressions. Further, we have also been exploring commitment over unreliable channels. Unreliability comes in two forms, viz., passive unreliability and active unreliability. The passively unreliable channel models are often poorly characterized, such that the exact channel characteristics remain obscure to both parties taking part in the commitment protocol. These channels are studied in information theory through the lens of compound channels and arbitrarily varying channels. Further, a stronger form of unreliability (“active” unreliability) comes into the picture if either of the two parties knows the exact channel behavior and can control the channel characteristics covertly, without the other party knowing about the same, to gain unfair advantage/information. Such channel models include Unfair Noisy channels (UNCs), Elastic Channels (ECs), and Reverse Elastic Channels (RECs). In particular, we have explored the commitment capacity of constrained DMCs, compound channels, and reverse elastic channels, which involves deriving a robust upper bound (converse) and designing computationally efficient and capacity-achieving commitment schemes. Our current work focuses on unifying all such channel models into a single frame of an unreliable channel model for studying commitment, which can reduce to different channels (compound, ECs, RECs, UNCs) under different conditions.

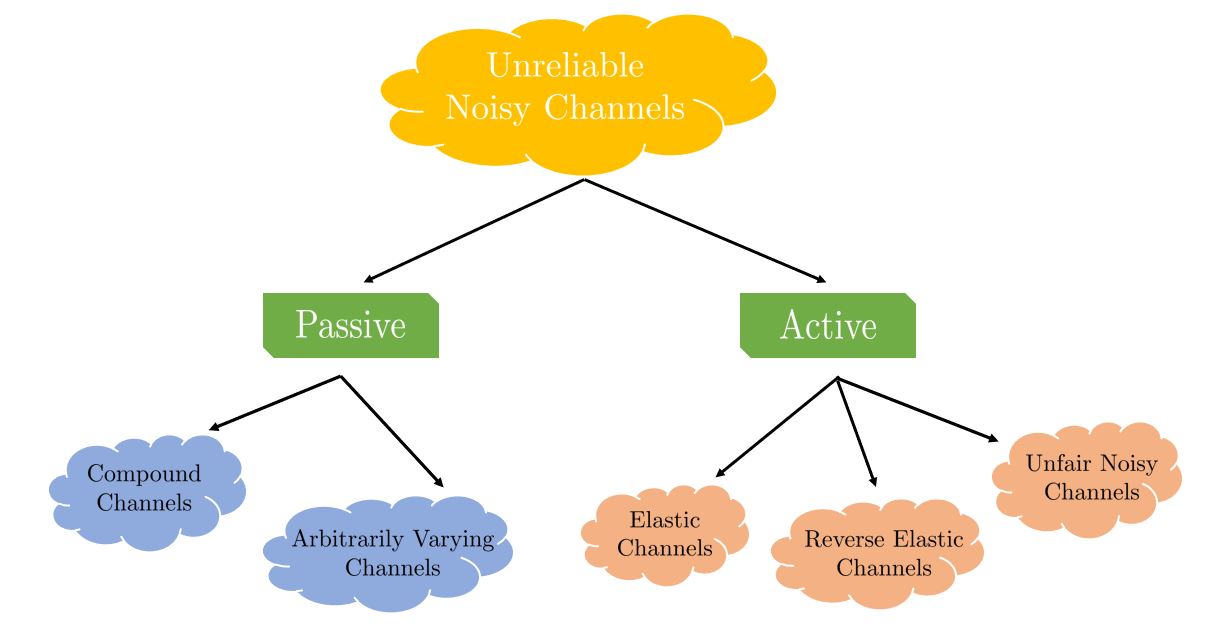
Example courtesy: [Winter et. al]
References: [Crepeau's webpage]

Oblivious Transfer

Oblivious Transfer (OT) is another interesting cryptographic protocol (closely related to Private Information Retrieval (PIR)) commonly implemented as a sub-protocol in multiparty computations, e-voting, etc. To better understand oblivious transfer, consider the following scenario: Eve is an employee who works in Alice's (employer) company. Bob is a detective (investigator) who suspects Eve of committing a crime. To carry out his investigation, he reaches out to Alice to gather information (data) about Eve's background. However, Bob wants to be assured that Alice doesn't get to know whose data he is seeking because if Alice does, it can jeopardize Eve's job in Alice's company if he later turns out to be innocent. Synchronously, Alice wants to be assured that Bob should “only” receive information/data of the employee that he seeks, not someone else's data, to maintain privacy.

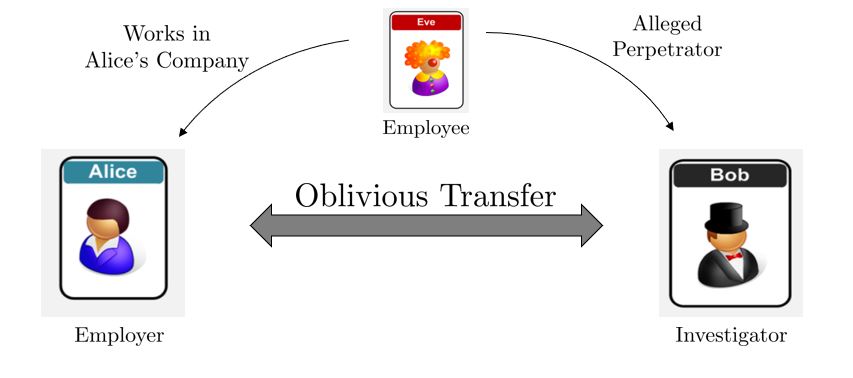
So, can this kind of functionality be achieved or implemented? The answer to this question takes us to Oblivious Transfer (OT) protocol!!

OT is an oblivious exchange of messages between two users. Similar to the commitment problem, our work is concentrated on implementing/realizing “unconditionally secure (information-theoretically secure)” oblivious transfer over noisy channels.

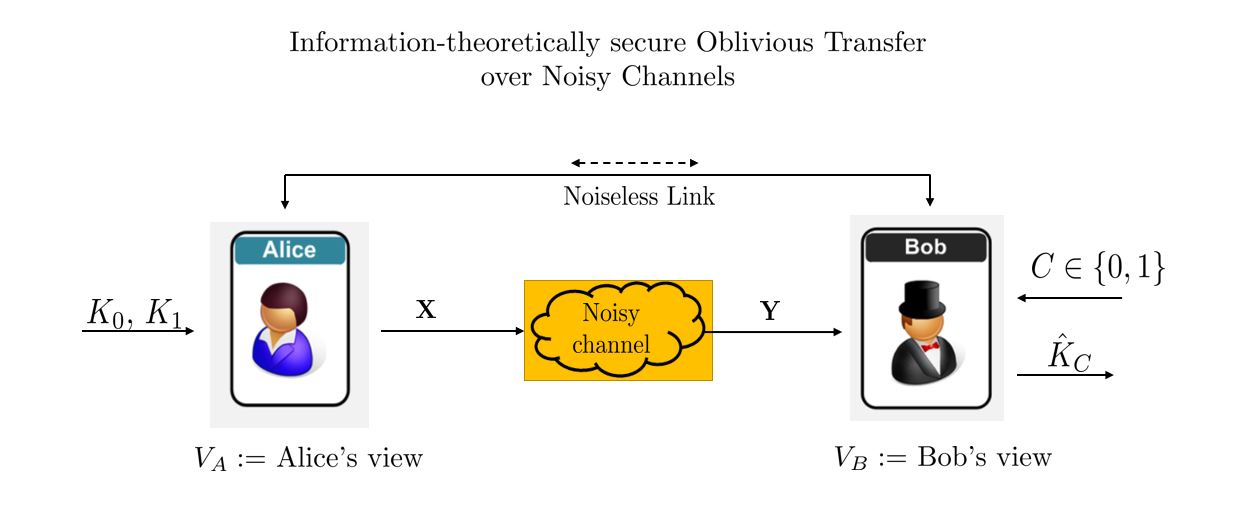
Specifically, we are studying OT over the class of unreliable channels. Currently, we are studying the (im)possibility results and fundamental performance limits of OT over compound discrete memoryless channels and its subclass of compound binary erasure channels (C-BEC). The OT capacity characterization involves providing a robust converse (upper bound) for OT rate and designing a computationally efficient OT scheme with a rate that achieves this upper bound. Furthermore, we are also currently exploring OT over adversarial channels (AVCs).

Secure Communication against Adversaries

A unifying theme underlying both adversarially robust communication and covert communication is the study of reliable information transfer in the presence of a strategic adversary. Although the two settings impose different constraints, they share a common departure from classical stochastic noise models and require coding schemes that remain effective under worst-case or adversarially chosen conditions. In the AVC framework, the adversary seeks to maximally disrupt communication by injecting carefully crafted noise, whereas in covert communication, the adversary aims to detect whether communication is occurring at all. Thus, the former focuses on ensuring reliability under malicious interference, while the latter simultaneously demands both reliability and statistical indistinguishability from pure noise. Together, these problems highlight the spectrum of challenges that arise when adversaries possess varying degrees of power, information, and observational capability, and they motivate the development of robust coding constructions, sharp (im)possibility results, and fundamental performance limits across diverse adversarial models.

Communication over Arbitrarily Varying Channels (AVCs)

The works of Shannon and Hamming in the mid-20th century led to the inception of information theory and coding theory, respectively. Though both fields are closely intertwined, the analyses made by Shannon and Hamming in their work were based on two completely different perspectives. On one hand, Shannon's analysis revolved around the stochastic (random) noise model to understand the trade-off between “rate” and “error” in communication, while on the other hand, Hamming's analysis was based on the worst-case noise to understand the trade-off between “rate” vs “distance” of a code. Today, more than 70 years after their developments, a lot is known about fundamental performance limits over stochastic (“average-case”) channels, which are part of Shannon's world. Contrastingly, in Hamming's world, we do not know much about the fundamental performance limits of channels with “worst-case” noise. This limits us to justify the optimality of the existing coding schemes in Hamming's world.

Our work focuses on bridging this gap between the two extremes of information theory and coding theory via the mathematical abstraction of arbitrary varying Channels (AVCs). It involves exploring fundamental performance limits as well as (im) possibility results and designing robust and optimal information processing schemes under malicious interference. Unlike the stochastic noise channels (such as discrete memoryless channels) as studied by Shannon, Arbitrarily Varying Channel models involve a potentially malicious third party, a.k.a jammer, who inflicts jamming noise “carefully” into the channel based on his observations or capabilities to disrupt the communication between the legitimate parties.

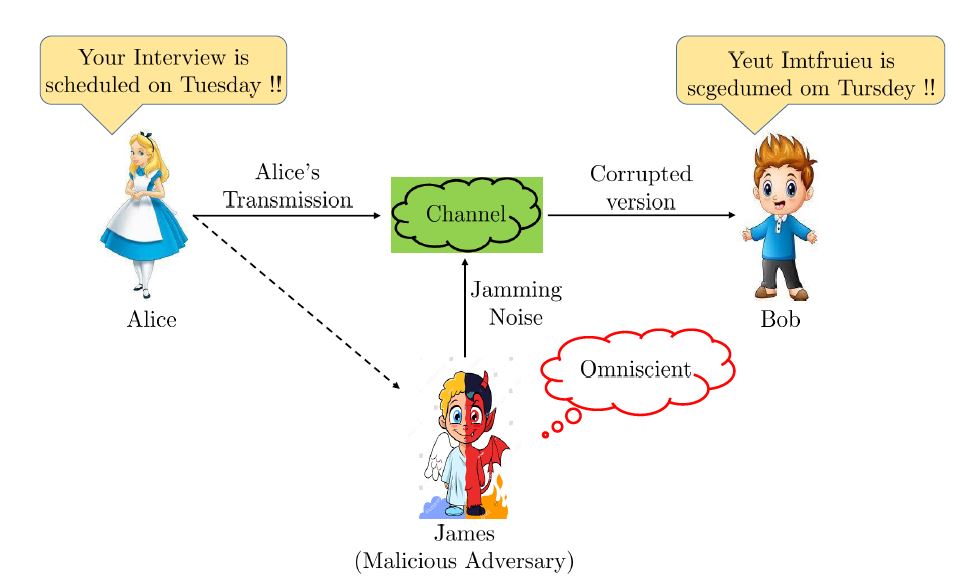
In our work, we are studying reliable communication in the most general scenario of a jammer modeled via omniscient arbitrarily varying channels (omniscient AVCs). The jammer in such channel models is omniscient to the sender's message, codebook, transmitted codeword, and the channel law and inflicts a jamming sequence (noise) into the channel based on these observations. Our goal so far has been to explore the (im) possibility results for communication over such channels and to study fundamental and achievable performance limits. We show that the communication over an omniscient AVC is possible iff it satisfies the “non-symmetrizability” condition. We have designed a cloud-code construction (inspired by satellite codes in broadcast channels) that achieves a large positive rate using a two-step decoder at the receiver. Furthermore, we have also derived sufficient conditions for omniscient AVCs under which simpler decoding rules, such as jointly-typicality decoding, MMI decoding, etc., suffice, and the code achieves the same positive rate as that by using a two-step decoder.

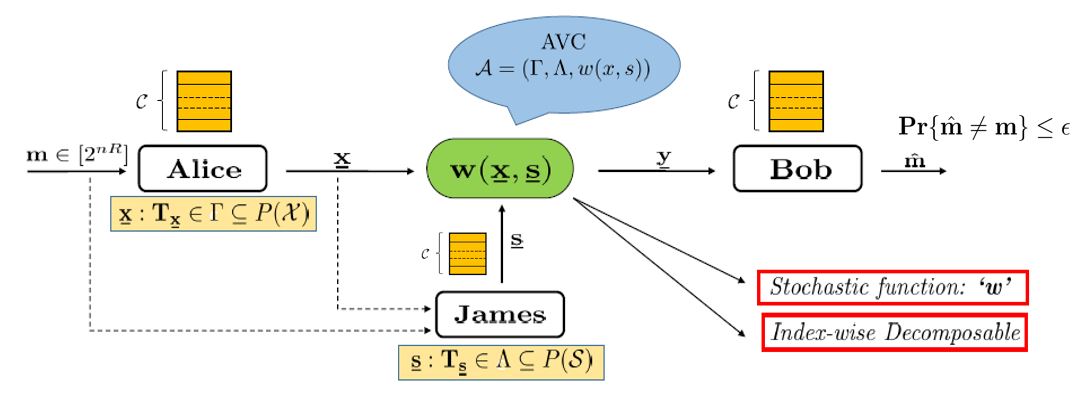
Currently, we are also studying communication over the class of “myopic” AVCs in which the jammer is comparatively weaker than that in the case of omniscient AVCs, and therefore, observes the noisy version of the transmitted codeword.

Covert Communication

Covert communication or communication with a low probability of detection or reliable-deniable communication is an exchange of messages between two or more users in a secret manner such that a third party or adversary doesn't even get to know if the parties are communicating with each other. To understand the problem, let's consider the following hypothetical example: Alice and Bob are criminals who are in jail but in different cells and want to exchange messages with each other such that the jailor of the jail (Eve) remains unaware of the fact that Alice and Bob are talking to each other.

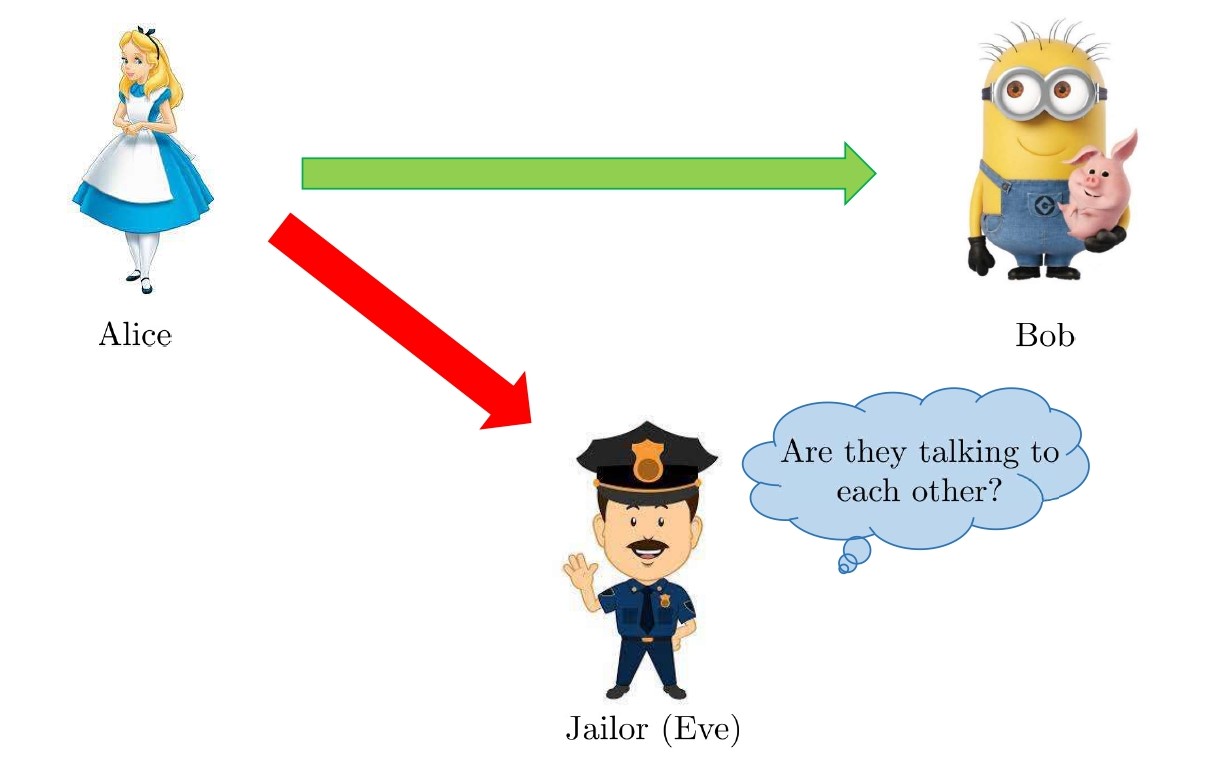
Noisy channels can be used as a significant resource for implementing covert communication. Mathematically, the goals in covert communication are as follows:

1). Reliability: The receiver, Bob, should be able to decode the message with low error probability (decreasing in block length n).
2). Deniability (Covertness): The adversary, Eve's observation, should be statistically close (eg, small KL divergence) to random noise (output distribution induced when the transmitter is not sending any message, i.e., off-input symbol, say 0 is transmitted).

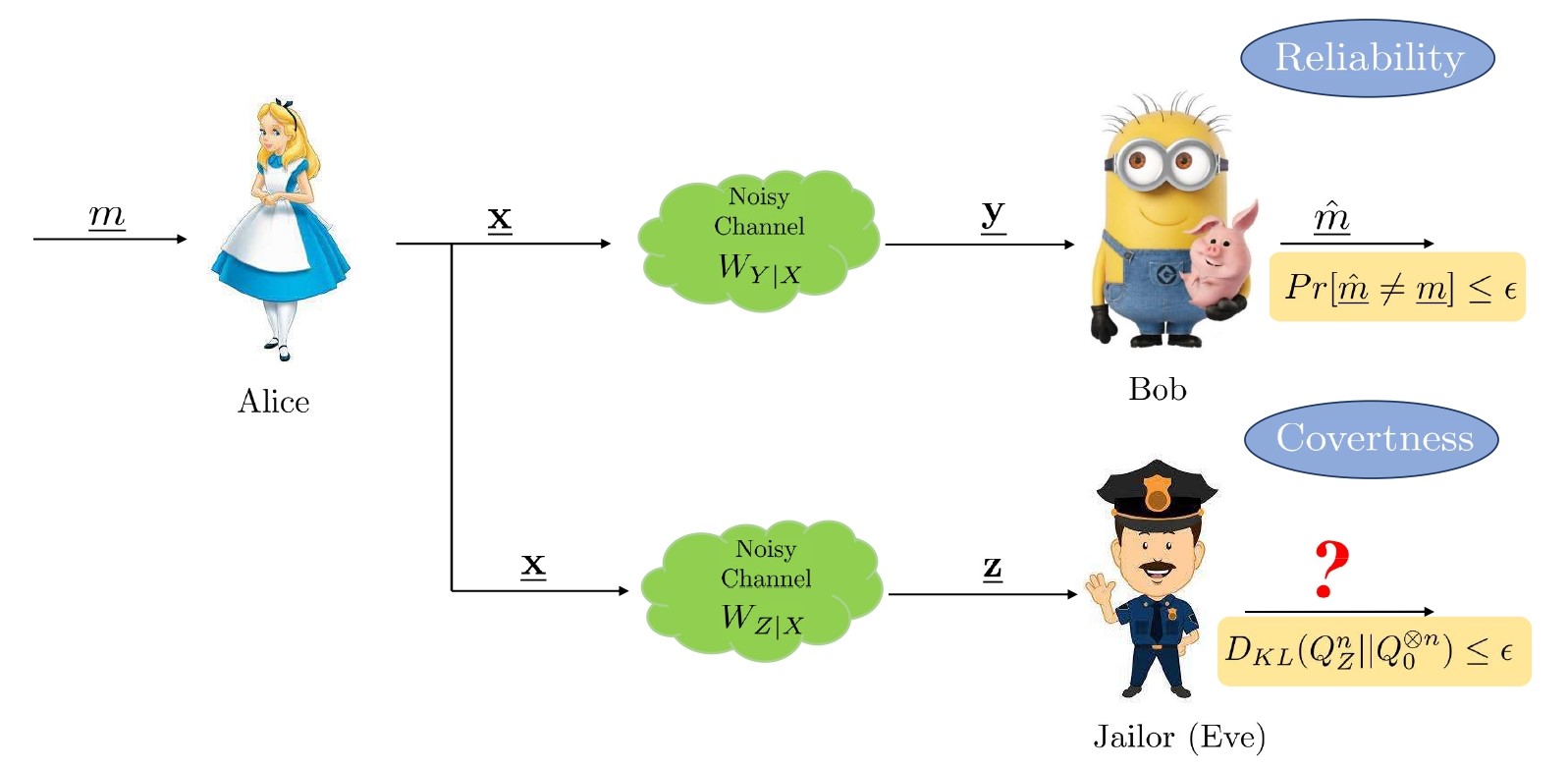
Several works have shown that covert communication over the different classes of channels including discrete memoryless channels (DMCs), as well as the additive white Gaussian noise (AWGN) channels, follows the square-root law i.e., the number of information nats that can be transmitted covertly (k) over the channel grows proportionally to the square root of the total number of channel uses (n). In such transmissions, both the conditions, i.e., reliability as well as deniability, hold. It has been recently shown that the Reed-Muller codes achieve capacity over any BMS (binary memoryless symmetric) channel in [RP21]. In our work, we focus on realizing covert communication over binary AWGN channels using Reed-Muller codes. We are currently working on showing that using Reed-Muller codes, both the conditions for the covert communication, i.e., reliability and covertness, can be achieved over a BI-AWGN channel such that the square-root law holds.